中学入試の出題例からみる求められる力
実際に中学入試で出題された問題を見ながら、受験生にどんな力が求められているのかを解説していきます。
特に有名私立中学では、4科目、国語・算数・理科・社会の基礎学力はもちろんのこと、これにプラスアルファの力が問われるのですが、どんな力が求められているのかを説明いたします。
中学入試は各学校、個別に試験が行われます。
試験ではその学校の校風や建学の精神が投影されている問題が出題されます。
そのため、受験生に求められる力とは、その学校が求めている人物像と言い換えられるかもしれません。
1. 国語 慶應湘南藤沢中等部
仮説を立て検証する道筋を考える力
ではまず、国語の出題例を見てみましょう。
慶応湘南藤沢中等部の入試で出題された問題です。
(160字以内)
グラフのひとつが日本のプロ野球選手の月別の出生数。
もうひとつが日本人男性の月別出生数(2016年)のグラフです。
プロ野球選手のグラフでは4月~7月の出生数が多いですが、一般男性の場合、月でほとんど差がありません。
みなさんはどのようにお考えになるでしょうか?
おそらくこの出題の意図は、4~7月生まれに有利に働くプラス要素であれば何でもよく、自分なりに考えて仮説を立てることと、それをどうしたら検証できるかを考える、そんな力を求めていると言えます。
たとえば、4~7月の温かい季節に生まれて、体を動かしやすいから運動能力が高められるのではないか、それを検証するには何をどう調べればよいかを考えて記述する、そういった問題になっています。
大学入試でいう小論文的な位置づけになると思いますが、発想の引き出しをどれだけ持てているかがひとつのポイントになるのかもしれません。
小学校の行事に主体的に取り組み、実体験からさまざまな発想が生まれるかもしれません。
家族で出かけるときも、どこに行ったのか、何を買ったのかの事実よりも、何をどう感じたかという経験が、子どもの感性を養うことにつながるかもしれません。
正解のない問いに対して、発想の引き出しを多く持ち、自分で論理を展開することが大切になってきます。
2.国語 フェリス女学院中学校
国語をもう1問、フェリス女学院の入試問題を見てみましょう。
これは先程の慶応湘南藤沢中等部の問題と異なり、前提となる論説文がこの問題の前にあります。
長文を読み解き簡潔にまとめる力
フェリス女学院の大問2番の問題で、大体5000~6000くらいの論説文を読んで、いくつかある設問のうちの最後に出題された問題です。
有名校の文章問題では5000~6000字の文字数は普通にあり、中学受験生はそれを乗り越えるために700~800字を1分間で読む、という速読力が要求されているともいわれています。
大人の平均が1分間でおよそ600~650字といわれていますので、大人の平均を上回るスピードで読み込んでこういった設問を解かなければなりません。
解答は200以内なので、原稿用紙の半分くらいですので簡潔にまとめる力も要求されます。
文章を書くためのいわゆる「テクニック」は進学塾で学習することになりますが、こういった問題を前にしてきちんと自分の考えを書けるようになるのは、簡単なことではないと思います。
先程と同じく机上の学習だけではなく、テレビを見る経験や外出先での経験の中で、日常生活をただ過ごすのではなく、疑問や興味が沸き起こったときにきちんとそれを調べてみたり、周りの大人に聞いてみたり、ご家庭の中での親子の会話の話題にすることで、自分の意見をまとめるための感性を養うこともできるかもしれません。
3.社会 慶應義塾普通部
慶應普通部の2022年度の社会で往復はがきの問題が出題されました。
「二重線で消すことば」と「書き換えたあとのことば」をそれぞれ書きなさい。
実際の入試問題では「慶應普通部行」という宛名が書かれた往復はがきの画像が描かれています。
日常生活の作法や習慣から学ぶ力
はがきの画像を見て二重線で消して書き換えることばは何か?という問題ですが、もちろん答えは「行」という字を「御中」に書き換えるわけですね。
大人からすれば、常識的なことですが、小学生にこの解を要求しているわけです。
先日、担当している算数の授業で、この問題を雑談程度に子どもたちに聞いてみました。
約20名の生徒の中で、この問題が正解できたのは1名だけでした。
まさにこの問題は小学校受験でも感じられる日常感が出ていて慶應幼稚舎であっても慶應普通部であっても、何か一貫した慶應魂みたいなものが感じられます。
普段の日常生活の中で学ぶべきこと、学べることがたくさんあるので、学びの機会を大切にしたいですね。
4.理科 麻布中学校
新型コロナ感染症の話題は中学入試では理科でも社会でも出題されていますが、今回紹介するのは麻布中学の2022年度の入試に出題された問題です。
大問4番の問題でリード文が長いので要約します。
私たちの体には無数の細胞があり、そのそれぞれに役割があります。仮に病原体が侵入したら、まず体の中の細胞が壊れますが、その一方でそれと対決する働きがあります。
(新型コロナウイルスの断面図を図示し)遺伝物質と、遺伝物質を元にして作られた表面タンパク質で包まれたウイルスを図で表します。
そしてこの病原体と対決する働きを免疫と言います。
免疫は(4)から(7)の順に進行します。
(4) 病原体の特徴を探る細胞が、病原体の表面の形状を読み取る。
(5) 読み取った形状を司令塔の役割の細胞に知らせ、司令塔からの働きで、読み取った形状にちょうど合う形の抗体がつくられる。
(6) 病原体は体内に無数にばらまかれた抗体とくっつくと、その場から動けなくなり、体内の異物を食べる細胞たちにやっつけられる。
(7) 司令塔となった細胞のいくつかは体内で生き残る。一度くっついた抗体の形を記憶しているので、同じ病原体が体内に侵入すると、すぐに抗体をばらまいて病原体をやっつける。
この問題のいくつかある設問の中の問5と問6を見ていただき、こんな問題が出題されているということを認識いただければと思います。
問6 ウイルス感染症は、(4)~(7)の働きだけでは治りません。その理由を答えなさい。(問題文一部抜粋)
疑問や興味を持ち自ら調べて学ぶ力
理科でも一問一答形式の知識を問うような学習も大切なのですが、最近の傾向では知識を前提として、こういった長いリード文や表、グラフを見てそこから解答を導くような分析力、思考力を要する問題が良く出題されています。
この問題には遺伝、ウイルスといったワードが出てきますが、これらは中学入試では出題の範囲外です。
中学入試の学習範囲では遺伝やウイルスに関する細かな知識を習うことはありません。
しかし、実際の入試では、こういった長いリード文を読む中で知識がなくても答えられる力、精読をした上で情報を正しく読み取り解を導くことができる力が求められていると思います。
特に理科においては身の回りの事象、たとえば気象や災害、防災といったテーマが多く出題されています。
普段から周りの事象に目を向けて、分からない言葉が出てきたら調べたり、実際にその場所に行ってみたりするなど、まさに理科本来の学び方を実践できているかを、改めて問われているように思います。
5.算数 フェリス女学院中学校
算数で問われる「思考」と「試行」の力
入試で出題された算数の問題について、私たちは毎年、「思考」と「試行」のどちらの性格の問題かを分類しています。
「思考」と「試行」、同じ読み方ではありますが、深く考えるという意味での思考と、手を動かすという意味での試行、またそれぞれをさらに2つに分けて全部で4つに分類します。

この中で2問、「思考」と「試行」の出題例を紹介します。
まず「思考」の例として本年度のフェリス女学院の算数の問題です。
1から100までの整数が書かれた100枚のカードに6の倍数に赤、4の倍数に黄色、7の倍数に緑のシールを順に貼り、別の色のシールが貼ってあったらはがしてから貼る、という手順が書かれています。
問われていることを理解する力
問題自体は丁寧に書かれていますので、きちんと精読すれば、算数の集合の単元の問題とわかると思います。
進学塾ではベン図や表を描いて整理していく解き方で訓練しますが、何が問われているのか、問題をしっかり読みとっていかないと失点につながってしまうため、「深く考える思考」が必要な問題の例として取り上げました。
算数の問題としてはよく見る典型問題なので、この問題をみて解き方がわからないという受験生はいなかったと思います。
また、100までの整数ですから全部の数字を書き出して、手を動かして解くこともできますね。
フェリス女学院では、こういった問題を前に手が止まってしまうことなく、自分で手を動かしてみる力、もう一つの「試行」の力のある子を求めているとも言えます。
6.算数 栄光学園中学校
もう1問、本年度の栄光学園の算数の問題です。
1から10までの10個の整数を1つずつ四角のマスに入れて分数の足し算の式を作ります。
設問(3)は、計算結果が7以下の整数になる式を1つ作り、計算結果の整数も答えなさい、という問題です。
粘り強く取り組む力
10個の四角に1から10までの数字を一つずつ入れるとてもシンプルな問題ですが、分数の足し算なので、通分が必要になってきます。
通分した上で計算結果が整数になるというのは意外と簡単ではありません。
しかも計算の結果が7以下になるという条件も加わっていますので、まずは答えが整数になるにはどうしたらいいか、という視点から始め、計算結果を小さい数字にするにはなるべく大きい数を分母にしよう、といった試行錯誤が必要になります。
この問題は非典型問題であり、見てすぐに解き方がわかる問題ではありません。
粘り強い計算が必要になるので、手を動かしながら、自分なりに分かること、うまくいく気づきを大事にして解いていく問題だと思います。
7.まとめ
ここまで受験生に求められている力を4つ取り上げました。

最後に、文科省のホームページからの引用ですが、学力の3要素について紹介します。
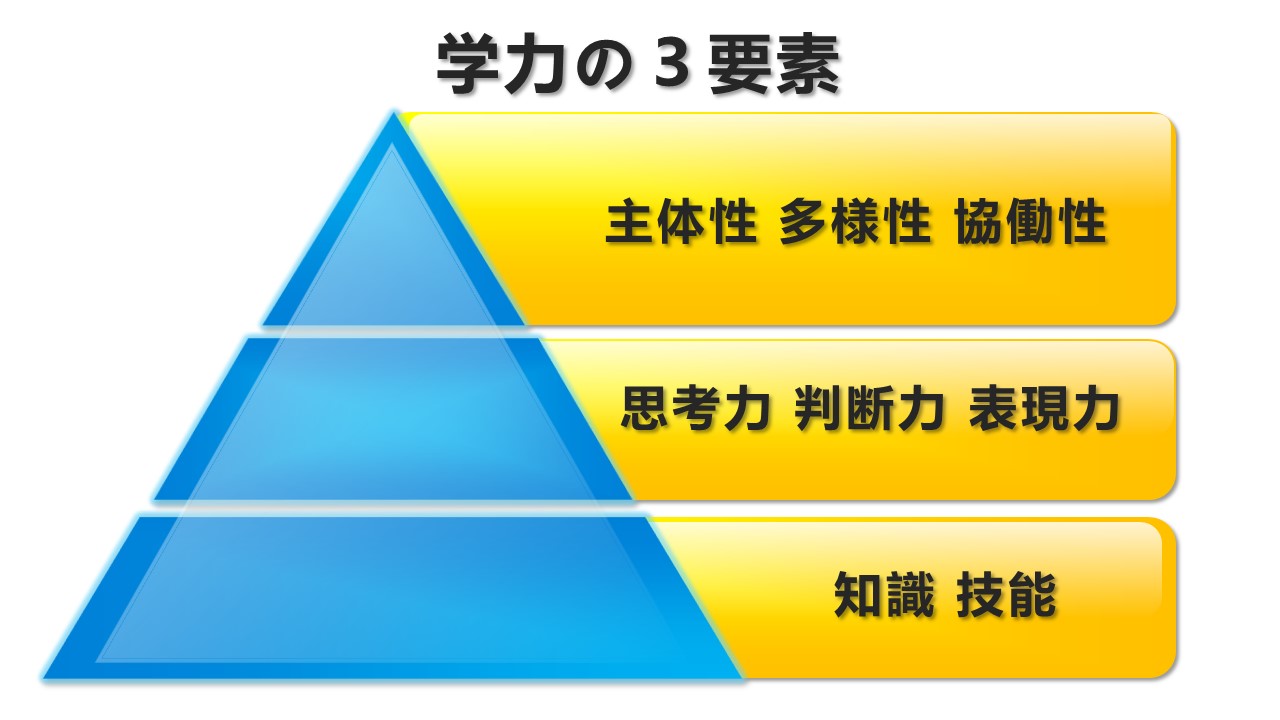
今まではピラミッドの一番下の知識・技能が学力と呼ばれていました。
先ほどのフェリス女学院の算数の典型問題などは、知識・技能に当たります。
その上の思考力・判断力・表現力は、「新学力」と位置付けられています。
先ほどの算数の非典型問題、その場で自分なりに論理を考えて進めていく問題は、この新学力に当たると思います。
知識・技能の指導については進学塾が一番得意としているところですが、新学力と言われているところは、幼児期からの経験や習慣から習得していくものではないかと感じています。
関連記事はこちら
国大Qゼミ中学受験コース 教務責任者