元号・西暦を使った問題
こんにちは。
中学受験コース算数科です。
いよいよ、2020年。
中学受験コースは、直前学習の時期となりました。
一生に1回しか経験できず、誰もが経験するわけではない中学入試。
だからこそ、この経験が次につながる良い思い出にして欲しいと思っています。
生徒全員が良い受験を迎えられるよう、最後まで全力でサポートしていきます。
今年は令和2年で西暦2020年。
やはり算数としては、「西暦・元号」を使った話題に触れたいと思います。
2020という数に関連した問題
2020という数字そのものに着目してみます。
数字の性質を見るには、素因数分解をしてみることが大切です。
素因数分解は『正の整数を素数の積の形で表す』ことです。
例えば、12=2×2×3となります。
2020はどうでしょうか。
2020=2×2×5×101と分解することができます。
こんな計算問題が出題されそうです。
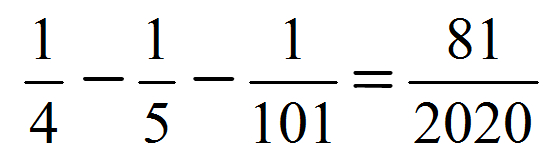 ※これはもうこれ以上約分できない真分数です。
※これはもうこれ以上約分できない真分数です。以下、2020に関連した問題を何題か想定してみます。
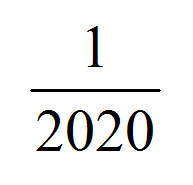 を小数で表したとき、小数2020位はいくつになりますか。
を小数で表したとき、小数2020位はいくつになりますか。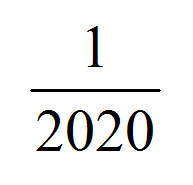 は、小数に表すと、次のような「きまり」が見えてきます。
は、小数に表すと、次のような「きまり」が見えてきます。
1÷2020=0.0004950495・・・(循環小数)
小数第3位以降、「0495」の繰り返し(周期)となっています。
(2020-2)÷4=504・・・2
周期の前から2番目なので
4(答え)
例えば、「9=2+3+4」と3個の連続した整数で表すことができます。
2020の場合の考えられる一例を挙げなさい。
これは、素因数分解 2020=2×2×5×101を活用します。
2020=404(平均)×5(個数)
2020=402+403+404+405+406(答え)
※ペアの和は奇数となる
101(ペアの和)×(40個÷2)
101=50+51より、2020=31+32+33+・・・・・50+51+・・・・・・・68+69+70(答え)
505(ペアの和)×(8個÷2)
505=252+253より2020=249+250+251+252+253+254+255+256(答え)
このとき、2020は前から何番目に登場しますか。
前から順に書いていくと、2,20,22,200,202,220,222,2000,2002,2020
10番目(答え)
※N進法を活用した解法もありますが、ここでは省略いたします。
0と2だけ使う場合、勢いよくケタ数が増えていくのですね。
書いてみるとあっという間に2020に到達することが分かります。
今年はいよいよ東京オリンピック・パラリンピック(東京ニーゼロニーゼロ大会)が開催されますね!
2020年もどうぞよろしくお願いします。
国大Qゼミ中学受験コース 教務責任者