みなさん、こんにちは！
受験算数を学び終えた教え子たちと久しぶりに会うと、懐かしい思い出話に花が咲きます。そんな中、私がいつもつい聞いてしまう質問があります。
「受験算数の中で、最後まで好きになれなかった単元は何だった？」

中学受験算数で好きになれなかった単元・ベスト3

これはあくまで私の感覚ですが、答えにはある程度の傾向がうかがえるので紹介しますね。

今回はその中で堂々（？）の第1位、「立体図形」の入試問題を取り上げてみたいと思います。
出題する問題は難関中学の過去問を改題した内容です。

1.立体図形の問題

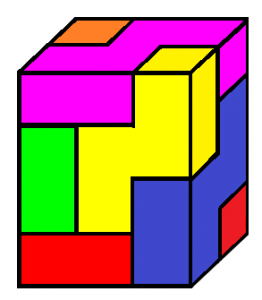
図の太線は、ある立体の展開図である。

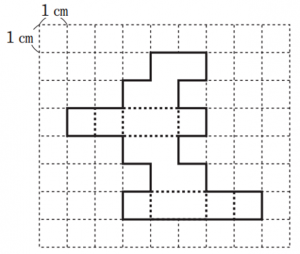
(1)この立体の体積を求めなさい。
(2)この立体を6個用いて、すきまなく組み合わせると直方体ができる。この直方体の表面積を求めなさい。

2.立体の体積の求め方

「展開図」とあるので、まずはこれを立体としてイメージする必要があります。
展開図を見ながら「同じ形の部分」に注目してみましょう。

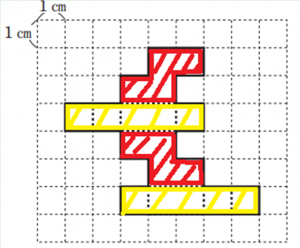
ポイントになるのは赤い部分と黄色い部分がそれぞれ同じ形だと気がつくかどうかです。
「これが底面（または側面）になるんだな」とピンとひらめけばOKです。

そして、同じ色の図形が向かい合うように頭の中で立体を組み立てていきます。

このような立体が思い浮かびましたか？


1辺1cmの立方体が4個組み合わさった、体積4㎤の立体ができました。

3.直方体の表面積の求め方

では（2）の問題です。
中学受験では、ここが得点できるかどうかの分かれ目です。

「この立体を6個使って直方体ができる」と書かれています。
「本当にできるのかな？」と疑いたくなる気持ちもわかりますが、問題文で「できる」と明言されている以上、まずはそれを前提に考えていきましょう。

ここでのポイントは、「完成形の直方体を具体的に思い浮かべない」ことです。
というのも、この独特な形の立体を6個頭の中で組み合わせて直方体を作るのは、かなり難しい作業だからです。
入試は時間との勝負。現実的な戦略とは言えません。

そこで発想を変えてみましょう。
体積から考えるのです。

この立体をどう組み合わせたとしても、完成する直方体の「体積」は同じになるということはわかりますよね。
1個4㎤の立体を6個使うので、体積は次のようになります。

4㎤×6個＝24㎤

つまり、体積24㎤になる直方体の「たて×横×高さ」の組み合わせを考えればよいのです。

可能性があるのは、次の6通りです。

（1）の立体を使ってすきまなく直方体を作るのですから、①〜④は除外されます。
なぜかというと、これらは「1cm×◯cm×◯cm」となっており、（1）の図形のの面を平面にならべて四角形に収めることになりますが、どう並べても四角形にはならないからです。
例えば、平らに並べてみるとこのようになりますが、上から見ると…

↓

どこかで1マス欠けるので、きれいな四角形にはなります。
となると、残りは⑤、⑥になります。

⑤をイメージしてみましょう。（1）の立体を組み合わせて6cmの辺を作ろうとしても、独特の形が影響して凹みなく6cmの辺を作ろうとしても上手くいかないことに気が付きます。つまり、⑤も不適切です。

そうすると、正解は**⑥（2cm×3cm×4cm）**の直方体ということになります。
あとはその表面積を求めるだけ。
（2cm×3cm＋2cm×4cm＋3cm×4cm）×2面＝52㎠
これが答えです。

4.まとめ

設問（1）の問題では、展開図から立体をイメージする力が求められました。
難易度としては標準レベルで、多くの学校の入試でよく出題されるタイプの問題です。

設問（2）は、一見すると（1）と同様に見取図をイメージして解く問題に見えますが、実は発想を切り替えて、体積から逆算して解くという論理的な思考が求められる、やや難易度の高い問題でした。

このような空間認識力を問う問題は、灘中など超難関校を除けば、それほど頻繁に出るものではありません。
したがって、複雑すぎる図形のイメージ力を身につけることに過度な心配をする必要はありません。
むしろ、「この問題、見た目通りに考えるより別の方法があるんじゃないか？」と気づく視点の切り替え、いわば“思考のスイッチ”を持っているかどうかの方が大切です。

出題される以上、問題には必ず正解へのヒントがあるはずだ――そう信じて思考を巡らせること、そのプロセスを子どもたちと共有することも、私たちがライブ授業で果たす大切な役割だと考えています。

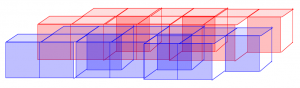
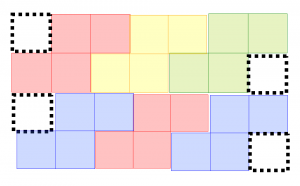
ちなみに設問（2）の立体を6個組み合わせた完成図も紹介しておきます。
それぞれ色分けされており、6個の立体が組み合わされていることが一目で分かります。

見てしまえば「なるほど」と思える図ですが、これを知らずに頭の中だけ（あるいは紙に描いて）でイメージするのは、やっぱりなかなか難しいですよね。