2024を使った入試予想問題
こんにちは。中学受験コース算数科です。
来年は令和6年の西暦2024年。
今年も年の瀬の話題として「西暦」問題をお届けします。
余談ですが,令和の年数に018(れいわ)を足すと、西暦の下2桁になる語呂合わせは知っておくと得するかもしれません。
例) 令和6年⇒6+18=24より2024年
1. 西暦2024
まずは「2」「0」「2」「4」という数字に着目して・・・
問題①
2024は「0」と「2」と「2」と「4」を使って表すことができる数字です。
(1)この4つの数字をすべて使って,四則計算の答えが10になる式を1つ作りなさい。
(2)「2024」のように「0」を1個、「2」を2個、「4」を1個使ってできる4けたの整数は何個ありますか。
~解き方のヒント~
(1)メイクテン(テンパズル)と呼ばれている遊びになります。「0」と「2」と「2」と「4」の場合,それほど難しくはないですかね。物足りない方に向けて,過去に中学入試に出題された問題を1題紹介しておきます。
「3」、「4」、「7」、「8」を使って、10を答えにもつ式を書きなさい。(2004年 開成中 改題)
※解答は記事の終わりに掲載しています。
(2)調べあげていく問題です。千の位が2のときと4のときを調べれば終わりです。
2. 算数では定石の「素因数分解する」ということ
素因数分解とは「正の整数を素数の積の形で表す」ことを言います。
2024を素因数分解するとどうなるでしょうか。
素因数分解をするときに、次のようなステップで検討を進めていきます。
STEP1 素数を順に書き出してみる
STEP2 2から順に2024を割ってみる
STEP3 順に割り算していき、割り切れた場合の商をさらに素因数分解していく。
そして、最後に商が素数になった時点で終了です。
1012÷2=506
506÷2=253
253÷11=23
※23は素数なので、これで終わり。
⇒2024を素因数分解すると、2×2×2×11×23
素因数分解が絡む問題として,下記のような問題が考えられます。
問題②2024年度に出題が予想される計算問題
![]()
~解き方のヒント~
1から順に□に数字をあてはめていくと意外とあっさりと答えが求まります。
また,素因数分解「2×2×2×11×23」の式を2つのグループに分けてみることも有効です。
素因数分解から,(2×2×11)×(2×23)=44×46を発見できれば,□にあてはまる数字が分かります。
また,45×45=2025となることは多くの受験生が知っていることなので,そこから求める方法もあります。
※小学生は「X2-Y2=(X+Y)(X-Y)」となる因数分解は未習です。
3. 約数はいくつある
2024を割り切ることができる整数は、かけ算の答えが2024となる式を書いて求めます。
⇒2024の約数は1,2,4,8,11,22,23,44,46,88,92,184,253,506,1012,2024
の16個ある。
これは、素因数分解
![]()
の指数に注目し、
![]()
16個と求めることもできます。
これに関連して,「約数の個数が16個となる最小の整数を求めなさい」などの出題も予想できますが,これは「120」が答えとなるので,難易度が少々高くなります。
4. 分数分解
2024を「20」と「24」と分解してみることで、次のような典型問題も考えられます。
「分数分解」とは、
![]()
など、分解して立式することで計算の工夫につながる話題です。
例えば、次のような計算をするとき、上の性質を活用することですぐに答えが求まります。
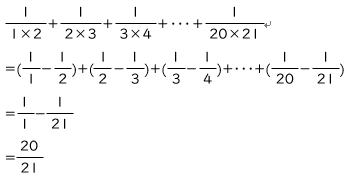
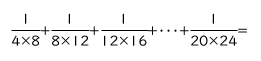
~解き方のヒント~
すべての分数を通分して計算することは厳しいですね。
上で記した分数分解の考え方を活用することで,一瞬で答えを求めることができます。
5. 定番の問題
算数の単元名の中で「周期算」というものがあります。
あるきまりで数字や記号がならべられていて、そのN番目が何であるのかを調べたり、N番目までの数字の和を求めるといった問題です。
下記の問題は、数字が「2024」になることで特別な技術が必要になるわけではありませんが、小問系の問題の中で出題が予想されます。
2×2×2のように2を3回かけた数の一の位は8です。2を2024回かけた数の一の位はいくつになりますか。
~解き方のヒント~
実際に2024回かけることは不可能なので,規則を見つけることが最優先です。
2を1回かけると一の位は「2」,2回かけると2×2=「4」,3回かけると2×2×2=「8」
4回かけると2×2×2×2=16(一の位は「6」),5回かけると・・・
問題⑤2024年度に出題が予想される「周期」に関する問題2

~解き方のヒント~
まずは分数を小数になおすところからスタートします。
5÷7=0.714285714・・・
規則(周期)が見つかったら,その周期が2024までに何グループあるのかを計算してみましょう。
さいごに
算数では、西暦・元号に関連する問題が出題されることがあります。今回は、その一部をご紹介しました。
今年の受験生は、2024=2×2×2×11×23であることは最低限、知っておいた方がよさそうです。
最後までお付き合いいただき、ありがとうございます。みなさま、良いお年をお迎えください。
そして2024年もどうぞよろしくお願いします。
国大Qゼミ中学受験コースでは本年度、「西暦・元号に関連する予想問題」を冬期講習中に学習します。