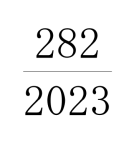2023を使った入試予想問題
こんにちは。
中学受験コース算数科です。
来年は令和5年の西暦2023年。
そこで、2023年度入試で出題が予想される問題を用意してみました。
1. 2023を素因数分解する前に
まずは「2023」という数字に着目してみましょう。
素因数分解※からスタートしましょう。
※素因数分解…正の整数を素数の積の形で表すこと
素因数分解をおこなえば、その数字が持つ性質を知ることができます。
2022は、2022=2×3×337と分解できました。
したがって、2022は2や3や337の倍数であることが分かります。
2. 2023を素因数分解するステップ
素因数分解をするときに、次のようなステップで検討を進めていきます。
① 素数を順に書き出してみる
23 29 31 37 41 43 …
② 2から順に2023を割ってみる
③ 順に割り算していき、割り切れた場合の商をさらに素因数分解していく
最後に商が素数になった時点で終了です。
289÷17=17
※17は素数なので、これで終わり。
素因数分解は、このような手順で進めていくしか方法はありません。
3. 2023を素因数分解すると?
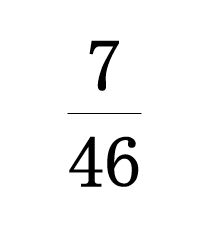
2022は、いきなり2で割り切れましたが、2023が7で割り切れることは知っておいた方が良いかもしれません。
その後、289が登場しますが、これは、受験生ならば平方数※であることはすぐに気づきます。
※平方数…同じ整数を2個かけた数字
「7(ラッキーセブン)」が3個ありますので、何だか幸運に恵まれる年になりそうですね♪
平方数に関連する問題も出題されそうです。
2023年度受験生は「11×11」から「19×19」までは知っておいた方が良いでしょう。
14×14=196、15×15=225、16×16=256
17×17=289、18×18=324、19×19=361
4. 2023を使った入試予測問題
ここからは、2023年度の中学入試に出題が予想される2023という数字まつわる問題を紹介します。
まず、分数計算の問題です。
① 2023の分数計算の問題
分母に7、17がからむ問題
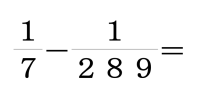
② 2023の約数の個数に関する問題
約数はいくつあるか?
2023を割り切ることができる整数を見つけます。
かけ算の答えが2023となる式を書いてみましょう。
7×289
17×119
これらを利用しましょう。
1、7、17、119、289、2023
6個と導き出すには、素因数分解 ![]() の指数に注目する方法もあります。
の指数に注目する方法もあります。
(1+1)×(2+1)=6個と求めることもできます。
これにもとづき、次のような問題が予想されます。
2023の約数は6個でした。
それでは、約数が6個ある自然数で小さい方から5番目の数を求めなさい。
③ 2023の分数分解に関する問題
2023を「20」と「23」と分解してみることで、次のような典型問題も考えられます。
「分数分解」とは、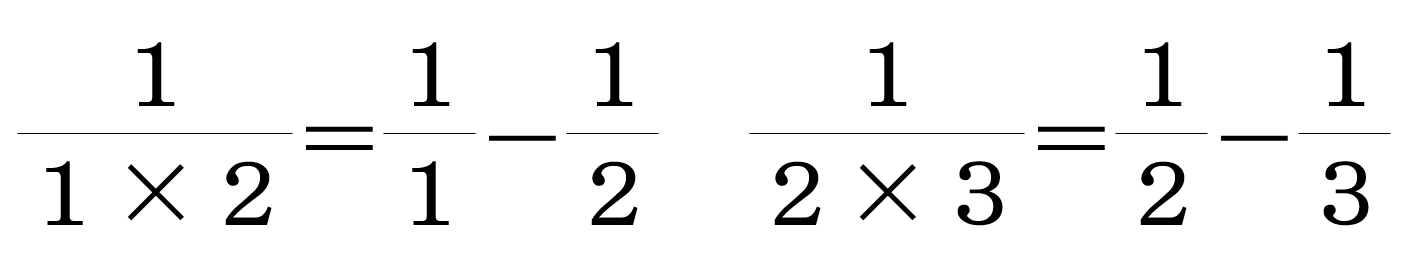 など、分解して立式することで計算の工夫につながる話題です。
など、分解して立式することで計算の工夫につながる話題です。
例えば、次のような計算をするとき、上の性質を活用することですぐに答えが求まります。
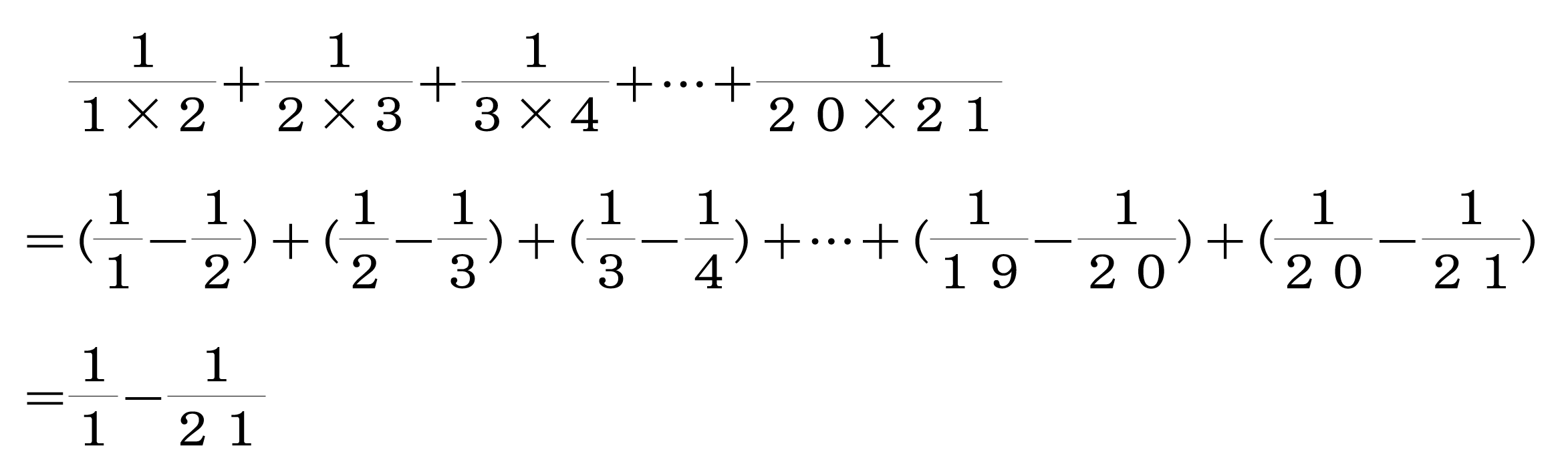
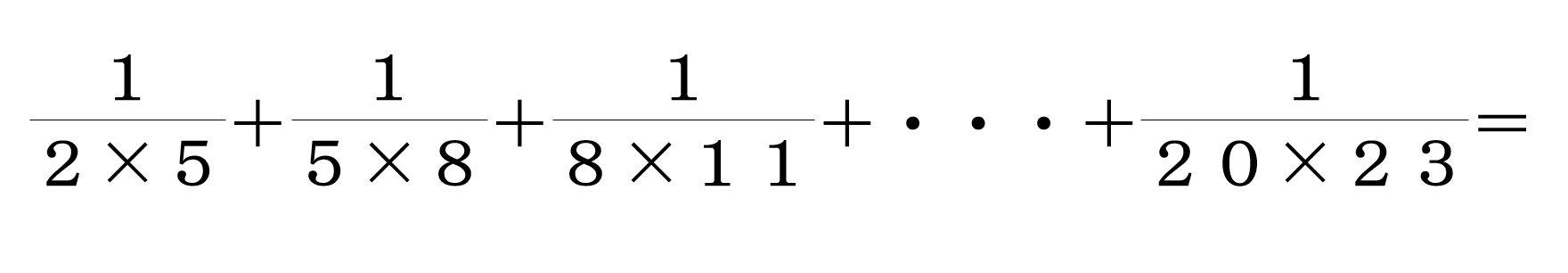
④ 2023の周期に関する問題
算数の単元の1つに「周期算」があります。
ある決まりに従って数字や記号が並べられています。
そのN番目が何であるのかを調べたり、N番目までの数字を和を求めたりといった問題です。
下記の問題は、数字が2023になることで特別な技術が必要になるわけではありませんが、小問系の問題の中で出題が予想されます。
2×2×2のように2を3回かけた数の一の位は8です。
2を2023回かけた数の一の位はいくつになりますか。
 を小数で表したとき、小数第2023位の数はいくつですか。
を小数で表したとき、小数第2023位の数はいくつですか。5. さいごに
算数では、西暦・元号に関連する問題が出題されることがあります。
今回は、その一部をご紹介しました。
今年の受験生は、2023=7×17×17であることは最低限知っておいた方がよさそうです。
国大Qゼミ中学受験コースでは本年度、「西暦・元号に関連する予想問題」を冬期講習中に学習します。
国大Qゼミ中学受験コース 教務責任者