2021年度中学入試を分析! いま求められている力とは？

こんにちは。
Qゼミ中学受験コース算数科です。

本年度、コロナ禍で実施された中学入試。
緊急事態宣言下で行われたこともあり、例年とは異なる対応が相次ぎました。

入試前の学校説明会はオンライン実施が多く、小学6年生でさえも自由に私学訪問できる状況ではありませんでした。
例年は入試前の訪問をきっかけにして直前学習への意欲を高めることができたのですが、今年はそれもかなわなかった受験生が多くいました。

入試要項の変更も相次ぎ、面接試験の中止や保護者控室の制限、学校によっては追試の設定など、直前まで動向を注視しなければなりませんでした。

入試中に控室に入れない保護者は近隣のお店や電車で数駅分離れたターミナル駅の構内カフェで時間を過ごした方もいらっしゃいました。

大変な中での入試でしたが、今年の受験生はそのぶん精神的に成長したのではないでしょうか。
この逆境での経験が次のステージでも様々な壁を乗り越える力になるでしょう。

さて、今回はそんな2021年度の入試問題をご紹介しながら、いま受験生に求められている力についてお伝えできればと考えております。

1．横浜雙葉中学校「問題文を自分で作る」

この問題文中にある2式はどこかで見たことがある式です。
売買損益算が話題であることも設問を見ればわかり、解きやすかったのかなとはじめは思いました。
ただ、式を吟味してみると1式目は割引をしていることに気付きやすいですが、その後、2式目で割り算をしているところで少し難易度をあげていると感じました。

ぜひ子ども目線で問題を見ていただきたいです。

2．浅野中学校「円周率の背景」

円周率とは、「オ」の長さが「カの長さの何倍かを表す数のことをいいます。
ただし、オ、カはそれぞれ漢字2字で答えなさい。
次に[図1]のように、半径1cmの円と一辺の長さが1cmの正六角形をかきました。
[図1]を参考にして、円周率が3より大きい理由を説明しなさい。

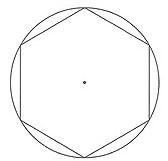
　　　　[図1]

円周率に関する問題は過去にも様々な学校で出題されています。
目新しい問題ではありませんが、円周率を当たり前のように使用している受験生にとっては円周率が「なぜ、そうなるのか？」と考えるきっかけになる問題ですね。

「オ」や「カ」のように言葉で説明させる出題も2～3年前から増えています。
毎年、話題になるような面白い問題が目白押しの浅野中学校。
他校で既に出題履歴のある問題を出題している背景を考えなければならないと思います。

「ネタ」が尽きてきたという言われ方も散見しますが、そんな安易な想像で終わらせるのではなく、1つ1つを「各駅停車」(浅野中学校の校訓)で背景まで理解して欲しい学校側の意図があるはずです。

また、入学試験としての適性を考えた場合、今までのような「視点」(解く糸口)自体の難易度をあげるのではなく、このような説明問題にすることで、日頃の学習姿勢をうかがい知れるということも想定されているでしょう。
参考までに円周率が4より小さい理由も算数では容易に説明ができます。
したがって「円周率が3より大きく4より小さい」という理由は算数で説明が可能です。

3．田園調布学園中等部「時流に沿った出題」

最後は、「キャッシュレス社会」を象徴する問題。
10年ほど前から「ポイントカード」にまつわる問題が出題されていますから、こちらも解く過程においては経験済みの受験生がたくさんいたことでしょう。
生活の中で馴染み深い問題ですが、受験生の正答率は如何に。

4．まとめ「新しい価値観をともなった学び」

今年の入試問題から三題取り上げました。
どの問題も、その背景は新しい時代への学びのとびらを開ける役割を果たしていると感じます。
このように、私たちが子どもの頃に経験してきた学習観とは異なる学びを実践することを要求されています。
そんなチャレンジをし続けている子どもを全力でサポートしていくことこそ、私たちの役割です。

過去の価値観だけをたよりに一方的な指導をしていく、そんな指導者がいるとすれば、子どもの思考を遮っていることになります。
まさに私たちも「当たり前をうたがうこと」を常に意識して、知識の伝達だけで終わらない双方向の授業を目指すこと、それこそがライブ授業の醍醐味だと考えます。

また新たに始まる1年。
子どもたちと共に、私たちも学び続けてまいります。
最後までお付き合いいただき、ありがとうございます。