算数を解くために必要なねばり強さ
こんにちは。
夏期講習の1か月は、今まで学習した内容を振り返り、さらに単元ごとの理解を深めていく大切な期間です。
算数を解くうえで必要な知識をおさえ、技術を磨いていくための問題演習が中心となります。
私は夏期講習にはもう1つ別の役割があると考えています。
初めて学ぶ単元が登場しない分、目の前の問題と向き合う「集中力」や「ねばり強さ」を身につけるということです。
通常期は単元の視点を知ることで精一杯な状況で余裕がないですが、講習はじっくりと向き合うだけの余裕があります。
1.覚える算数から考える算数へ
なぜ「集中力」や「ねばり強さ」を養う必要があるのか。
それは、「覚える算数」から「考える算数」へ移行して欲しいと思っているからです。
授業中に「解き方を忘れた」とか「この問題、習っていない」という発言をする子どもが多数いますが、算数に向かうスタンスとして根本的に勘違いしています。
『算数ができる子』と『算数が苦手な子』
その思考方法やスタンスには大きな違いがあります。
算数には、問題を解くために必要ないくつかの視点(普遍的な考え方)が存在します。
それは、数学ほど多いわけではありませんが、理解を深め、自分で使えるようになるまでに時間を要する場合がほとんどです。
言うまでもなく、単に公式に数字をあてはめ、それによって正解を楽しんでいる状況では、本当に「算数がわかった」こととはかけ離れてしまいます。
なぜならば、その視点はその場限りで忘れてしまい、原理を理解していないと思い出すことは不可能だからです。
算数ができる子は、公式を無理に覚えようとはしません。
なぜならば、覚える必要がないくらい、理解・納得を試みるからです。
心の底からわかった視点ならば、仮に忘れたとしても何とか自力で導き出すことができるわけです。
2.五角形の対角線の本数の求め方
例えば、対角線の本数を求める視点があります。
対角線は「多角形の異なる2点を結んだ線のうち辺をのぞく線」で、以下のようなものです。

四角形の対角線の本数は2本
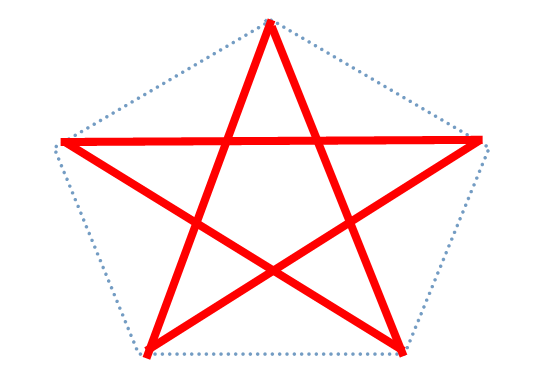
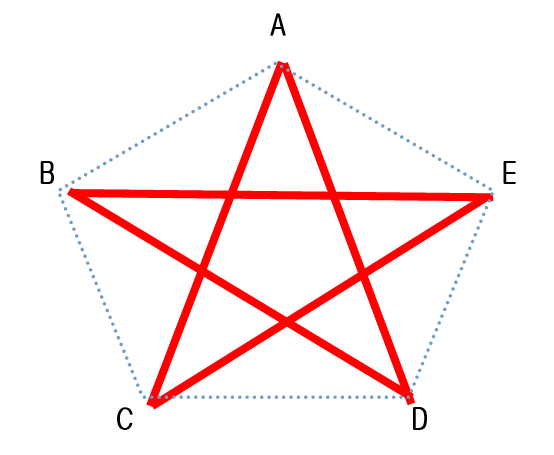
五角形の対角線の本数は5本
一般に□角形の対角線の本数は、次のように求めることができます。
(□-3)×□÷2
上の図で五角形は5本でした。
この視点を活用すると、(5-3)×5÷2=5 と求めることが可能です。
「算数ができる子」は、公式の背景に目を向けます。
五角形の場合を例にして簡単に説明してみます。
これは、Aのとなりの頂点B・EとA自身にはひくことができないため、5-3=2本であることがわかる。
五角形は頂点が5つあるので、1つの頂点から2本ずつひくと、2×5=10本となる。
10本の対角線を引いてみると、例えば、AからCにひく線とCからAにひく線が重複するため、最後に2でわる必要がある。
したがって、五角形の対角線の本数を求める考え方は、(5-3)×5÷2=5(本)とわかる。
※国大Qゼミ 小5算数教材
「小5サクセス演習編上巻 第6回解説」より
3.まとめ
このように一歩立ち止まって背景の理解を試みることができるかどうか、これはかなり重要です。
もしかしたら、小5の段階では理解できないかもしれない、しかし、そういった学習法を心がけることで、次に出会ったときにはより理解が深まっているはずです、
算数の目的は「目の前の問題に真剣に向き合いながら解く」ことで、「正解すること」ではありません。
中学入試本番で正解すれば良いだけです。
人から教わって正解するのではなく、自力で何とかクリアしていく瞬間をどれだけ積み重ねていけるか、あたかも自力で解けたかのように演出することもライブで行っている授業の役割です。
自分で考え続けることの大変さや、他人の力を借りずに解けたときの達成感も味わって欲しいと思いながら見守っています。