
図形を語らずして中学入試は語れない!
こんにちは。
私立中学に進学した教え子が、「数学は代数と幾何に分かれて授業があるんだね!」と話していました。
算数では分野によって授業が分かれることがないため、驚いたようです。
算数では、代数と幾何という表現はしません。
あえて、算数を分野ごとに分けてみると、次のようになります。
② 速さ 旅人算・通過算・時計算など
③ 割合 比・食塩水・売買算など
④ 文章題 つるかめ算・消去算・過不足算など
⑤ 図形 平面図形・立体図形
さて、みなさん、これらの単元の中で、中学入試で最も出題頻度の高い分野どれだと思いますか?
もっと言うと、どの中学校でも必ず入試に出る分野はどれだと思いますか?
それは、「図形」です。
図形を語らずして入試算数を語ることはできないのです。
特に平面図形は、面積を求めたり、相似に着目したりと様々な視点から取り組むことが求められます。
ですから、受験生にとっては入試成功のポイントになります。
そこで今回は平面図形の問題を1つ取り上げてみます。
鎌倉学園2014年3次試験(改)
長方形ABCDの中に四角形EFGHがあります。
このとき、長方形EFGHの面積は何㎠ですか。
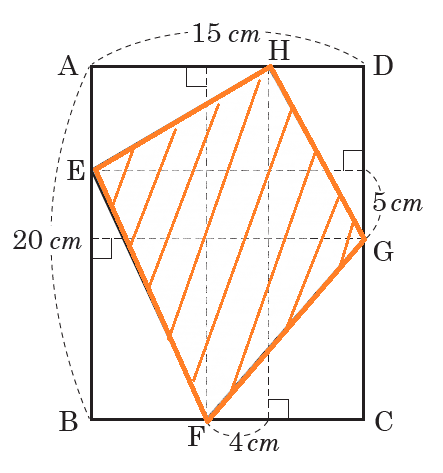
たまたま鎌倉学園の問題を選びましたが、これは中学入試ではよく出題されるタイプの問題です。
算数オリンピック※でも出題されたこともあります。
※算数オリンピック : 1992年より毎年開催されている、小学校以下を対象とする国内の算数コンテスト
中学受験生なら小4でも十分に解ける問題です。
実際、30秒ほどで解いてしまった4年生がいました。
やってみよう!という方は2分以内を目安に解いてみてください。
スマホのタイマーをセット!
でも先にポイントをお伝えしておきます。
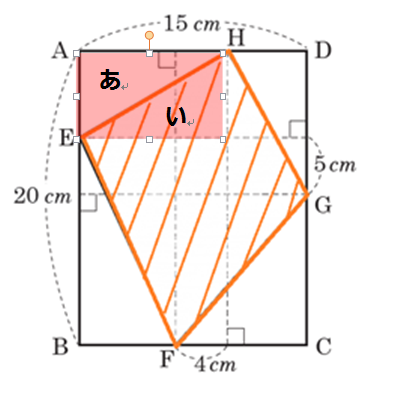
注目①
20㎠ですね。
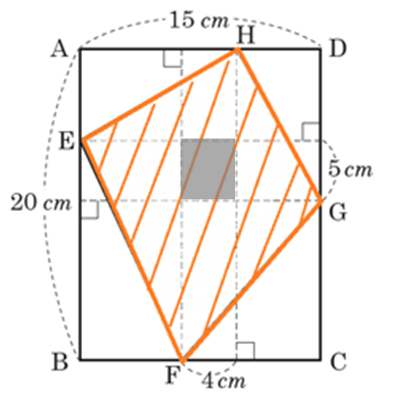
注目②
ここだけでは具体的に何㎠かはわかりませんが、「あ」と「い」は同じ面積=「あ」はオレンジ色の長方形の半分、であることがわかります。
注目③
周囲の長方形すべてに注目すれば、具体的な面積が求められますね。
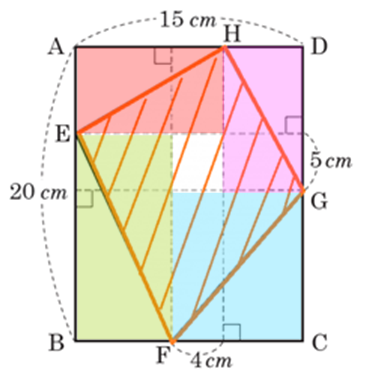
こうするとさらに見やすいでしょうか。

いかがでしょうか。
140㎠の人。
惜しいです!
中央の小さな長方形の処理を忘れてしまいましたね。
正解は160㎠
解き方は以下の通りです。
中央の小さな長方形 4×5=20㎠
長方形ABCD-中央の小さな長方形 300㎠-20㎠=280㎠
それを半分にしたものが4種類の三角形の面積なので 280㎠÷2=140㎠
最後に中央の小さな長方形の面積を加えれば、長方形EFGHとなる
140㎠+20㎠=160㎠(答)
今回のポイントは 「同じ部分に目をつける」でした。
これは、図形問題だけでなく、食塩水や速さなどの文章問題でもよく活用される視点です。
算数では、「同じ」「等しい」「一定」「変わらない」など、表現を変えてさまざまな場面で使われます。
このような分野を横断する視点を知ることで、解法を覚えることから解放されるのです
それでは、また次回をお楽しみに。








